Artiklen beskriver statistikkens rolle som videnskab. Begrebet kurtosis og dets brug i videnskaben overvejes.
Statistik. Grundlæggende koncept
Statistik er den grundlæggende afledning af matematisk videnskab. Dette fag hører til en række sociale discipliner, der har til formål at danne et billede af verdensbilledet og en kompetent analyse af begivenheder hos elever.
Statistik studerer alle slags processer og begivenheder i menneskers liv, fremhæver deres mønstre og præsenterer alt i form af korte statistiske rapporter. Sådan videnskab er soci alt nyttig og kræver konstant forbedring. Overskud - hvad er det? Dette er et grundlæggende koncept i grafisk statistik, der hjælper med at bestemme rigtigheden af perfekt regning. Kurtosis bør ikke have en stærk afvigelse.
Statistik giver dig mulighed for at tilfredsstille folks behov for pålidelig information om et bestemt fænomen, begivenhed og så videre. At bestemme dynamikken i livsfaktorer, deres tilbagegang, stagnation eller vækst - det er præcis, hvad denne videnskab gør.
I den moderne verden indtager statistik en af hovedpladserne på den videnskabelige arena. Lad os overveje begrebet "kurtosis". Hvad er et statistisk mål og observation? Hvor anvendes disse begreber? Læs mere om alt dette iartikel.
Hvad er kurtosis i statistikker?
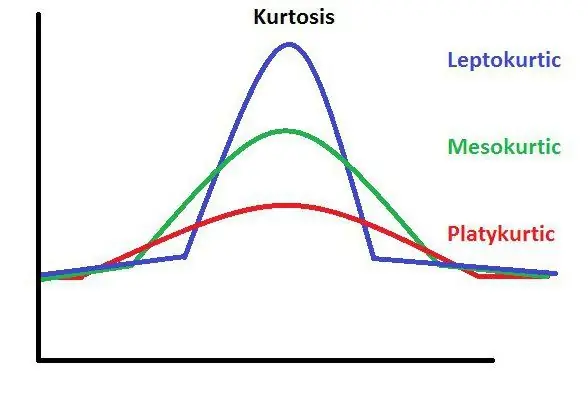
Kurtosis er et statistisk koncept, der repræsenterer skarpheden af hver top i en distributionsgraf. Der er en speciel formel for dens nøjagtige beregning.
Forventning siger, at for en mere jævn fordeling af statistiske data skal kurtosis være lig med et positivt tal. Bogstaveligt t alt betyder dette koncept en vis afvigelse fra normen og yderligere unormal udvikling eller funktion af det statistiske system.
Overdreven udtryk for kurtosis på en statistisk graf kan indikere en forkert undersøgelse eller fejl i grafens oprindelige data. Et sådant begreb er skalært af natur, hvilket betyder, at den endelige beregning skal resultere i et tal, der ikke vil indeholde variable eller hjælpefunktioner. Sådan ser kurtosis ud.
Hvad er symmetrisk og asymmetrisk fordeling
Kurtosis, som er relateret til fordelingen af den symmetriske type, er lig med nul. Dette kan tydeligt vises med en graf. Den asymmetriske graf viser et tal, der ikke er nul. Sådan betegnes kurtosis.
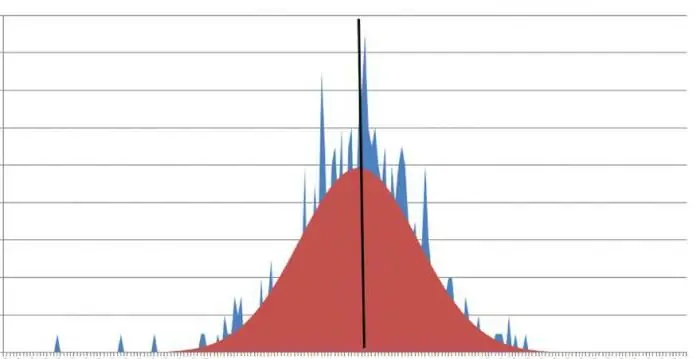
Hvad er skarpheden af en top? En graf, der har skarpe toppe, indikerer, at kurtosisværdien er et tal mindre end nul. Ofte er der situationer, hvor et givet begreb ikke kan udtrykkes med en separat værdi. I dette tilfælde nærmer det sig minus eller plus uendeligt.